Matemáticas

¿Qué es una derivada?

Es una medida de cómo cambia una función matemática en relación con su variable independiente. 

 Es como una especie de "pendiente instantánea" de la gráfica de la función. 

• Cálculo: Se toma una función y se calcula la pendiente de la recta tangente a la curva de la función en un punto específico, esto mediante el uso de reglas y fórmulas derivadas, como la regla del poder, la regla de la cadena y la regla del producto.

¿Qué es una segunda derivada?

La segunda derivada de una función es simplemente la derivada de la derivada de la función. Es decir, así como la primera derivada mide la velocidad a la que la función original cambios, la segunda derivada mide la tasa a la que cambia la primera derivada. La segunda derivada nos ayudará a entender cómo la tasa de cambio de la función original está cambiando en sí misma.

Ejemplo: La función f(x)=x^3+2x^2. Su primera derivada es f'(x)=3x^2 +4x. Para encontrar su segunda derivada, f'' necesitamos diferenciar f'. Al hacerlo, encontramos que f''(x)=6x+4 

Aplicaciones

Derivadas:

Segunda derivada:

- Determinar la concavidad de una función. 

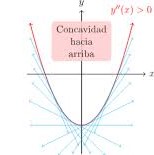
• Función cóncava hacia arriba: Si la segunda derivada es positiva en un intervalo, la función es cóncava hacia arriba en ese intervalo. Esto significa que la gráfica de la función se curva hacia arriba.
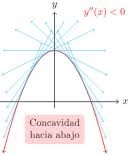
• Función cóncava hacia abajo: Si la segunda derivada es negativa en un intervalo, la función es cóncava hacia abajo en ese intervalo. Esto significa que la gráfica de la función se curva hacia abajo.

  Dada la función f(x)=x^ 3+3x^ 2+2 

• Calcular la primera derivada para observar el cambio de la pendiente                                     f′(x)=3x^ 2+6x
• Hallamos la segunda derivada para analizar la concavidad  f′′(x)=6x+6
• La concavidad depende del signo de la segunda derivada:                                  

Si f′′(x)<0 la función es cóncava (cóncava hacia abajo).                                                                         Si f′′(x)>0 la función es convexa (cóncava hacia arriba).

• Para este caso, f′′(x)=6x+6, se observa el signo:

Para x> -1 f′′(x)>0 por lo que la función es convexa (cóncava hacia arriba) en ese intervalo.

Para x<−1 f′′(x)<0 por lo que la función es cóncava hacia abajo en ese intervalo.

• Así, concluimos que la función cambia de concavidad en x=−1 y es convexa cuando x>−1

• Ejercicios de ejemplo de función cóncava hacia abajo:                                                    Dada la función g(x)= -x^2 + 4x

• 1. Calcular la primera derivada de la función:

     g′(x)=−2x+4

  2.  Calcular la segunda derivada para verificar la concavidad:

     g′′(x)=−2

  3. Se observa que g′′(x)=−2 es un valor constante y negativo. Esto indica que:

     • g′′(x)<0 para todos los valores de x, por lo tanto, la función es cóncava hacia abajo en todo su dominio, esto debido a que su segunda derivada es negativa en todo su dominio.

Hallar la concavidad de la función ayuda a:

• Visualizar la gráfica: Hacernos una idea general de cómo es la gráfica de una función sin necesidad de graficarla.
• Encontrar puntos de inflexión: Puntos donde la concavidad cambia.

https://es.khanacademy.org/math/ap-calculus-ab/ab-differentiation-2-new/ab-3-6/a/second-derivatives-review

https://espanol.libretexts.org/Matematicas/Libro%3A_Calculo_activo_(Boelkins_et_al.)/01%3A_Entendiendo_la_Derivada/1.06%3A_La_Segunda_Derivada